Flash Story
 Dr Babu Jagjivan Ram Housing Scheme Karnataka 2025 – Get Rs. 2.50 Lakh Assistance for Leather Artisans
Dr Babu Jagjivan Ram Housing Scheme Karnataka 2025 – Get Rs. 2.50 Lakh Assistance for Leather Artisans
 SBI Asha Scholarship 2025, eligibility, benifits, how to apply online, application form
SBI Asha Scholarship 2025, eligibility, benifits, how to apply online, application form
 Realme P4 5G Diwali Dhamaka Offer – Get a 7000mAh Battery 5G Smartphone for Just ₹16,999 | Realme P4 5G Price Drop, Features & Full Specifications
Realme P4 5G Diwali Dhamaka Offer – Get a 7000mAh Battery 5G Smartphone for Just ₹16,999 | Realme P4 5G Price Drop, Features & Full Specifications
 New Ration Card Apply Online Karnataka
New Ration Card Apply Online Karnataka
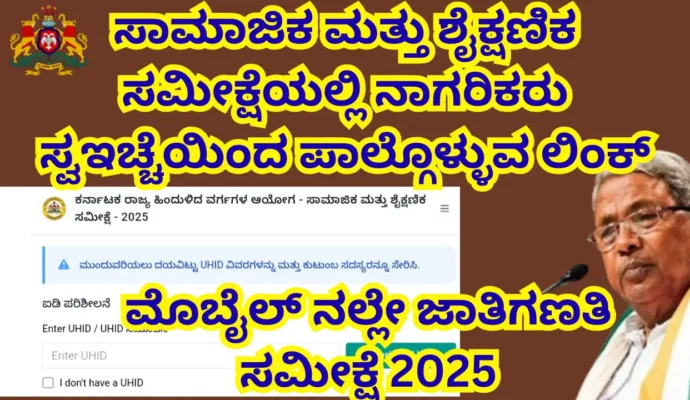
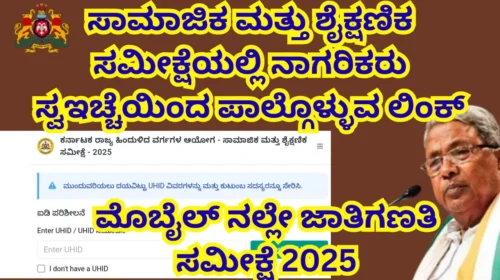 Caste Survey 2025 Karnataka Government Releases Official Website Link for Mobile Self-Survey
Caste Survey 2025 Karnataka Government Releases Official Website Link for Mobile Self-Survey